前言

在考慮 Facial landamrk 的模型時，我們直觀上確實可以考慮就拿一個 CNN backbone 去把一張照片壓成一條 feature 然後接上一條fully connected layer 去輸出 192 維的結果 (98個點, 每個點有 x, y)，而這個我們稱為 direct 方法。但一定要這麼做嗎？其實我們可以用 heatmap based 的方法去預測這個點，這個關鍵點就是這個 heat point 的中心點！而這個類型最有名的模型就是 Hourglass 的結構！那今晚我們就來介紹這個模型吧！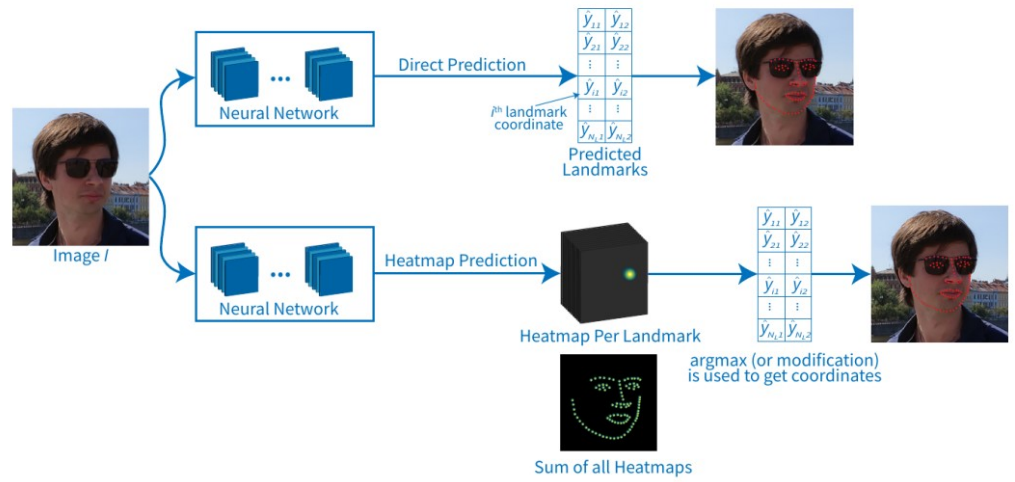

Heatmap as Landmark?

我們首先看看下面的例子:

假設我們想要去預測這個網球的位置，我們應該怎麼做?一個蠻直覺的作法就是去使用direct方法，就是一個 CNN 當作 backbone，然後接著fully connected layer 去預測這個網球的位置 (x,y），如下圖：

那 Heatmap based 則是去預測整張圖每一個地方為網球位置的機率圖，如下圖: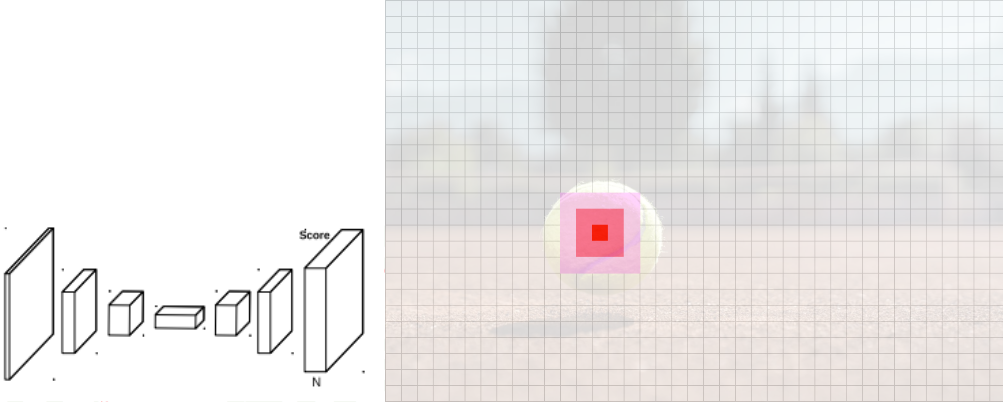

會使用到的結構為一個 CNN 負責壓縮整張圖然後做 upsample 慢慢放大回原本輸入的大小，其上的值為每一個點是網球位置的機率值，此時用 argmax 就可以得到預測的位置!

注意，通常會是每一個關鍵點都會是獨立預測出一張機率圖，然後再把這些機率圖處理後疊在一起

而這個結構最有名之一的就是 Hourglass 結構，是 2016 年University of Michigan的研究員發在 ECCV 會議上的結構，結構可參考下圖：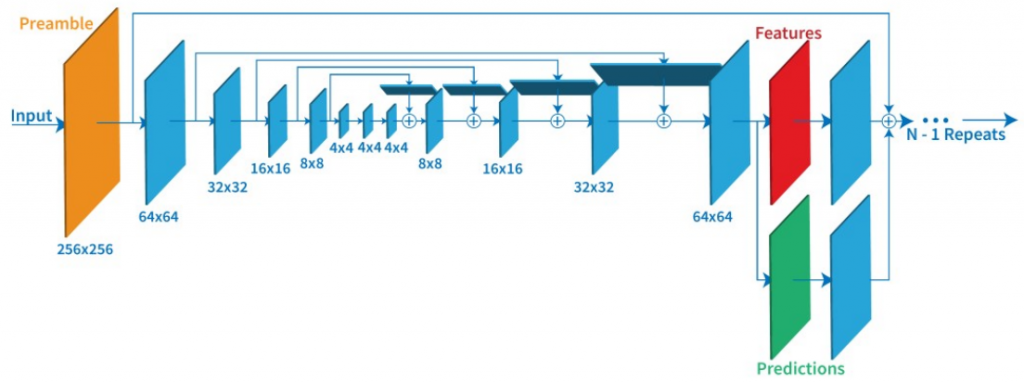

大家看到這個結構是不是覺得有點神奇，他竟然不像是 direct 那種一張圖進去後每一層的結果會越來越小的樣子，而是最後竟然又放大了! 沒錯這個結構就是 Encorder-decorder 類型的結構，而這也是 Hourglass 的命名由來---兩端大中間小的樣子是不是像極了沙漏 (Hourglass)
此時你可能心中會有一個大膽的想法?既然會放大回來，那是不是可以再接一次呢? 沒錯！當初 2016 年University of Michigan的研究員就是這麼想的!他們提出的網路結構就是一堆上面的結構--Hourglass bolck 所組成的樣子，如下圖: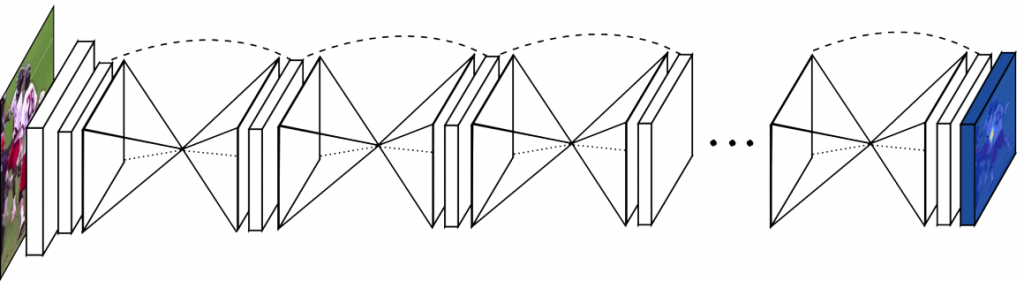

Why heatmap based?

上面提出的 Hourglass 最早是為了人體姿態這個 task 而提出的，就像下圖:

圖中模型在輸入一張圖片之後分別去預測左手腕的機率圖跟右手腕的機率圖然後在合在一起。
而人們驚奇的發現這樣做效果竟然出奇的好!比 direct 准了好多!如下表: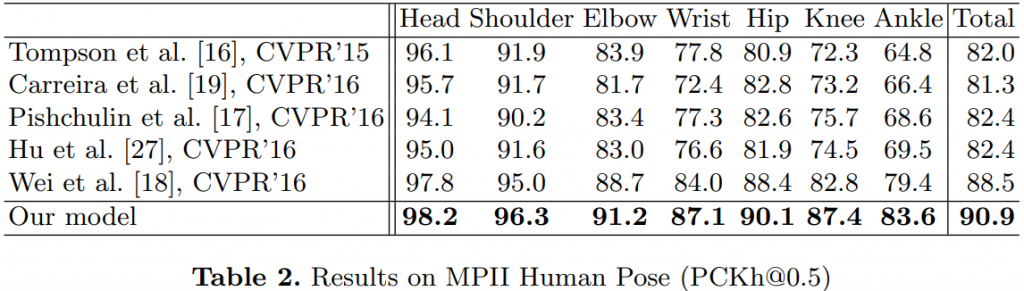

表中為測試人體關鍵點的準確度，數字越高越好!
而厲害的是，這個結構放在其他領域裡竟然一樣會比較好，像是在這篇論文中的實驗：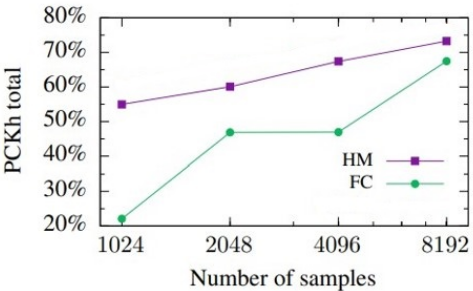

縱軸數字為準度越高越好!
其中， FC 就是 fully connected layer 的 direct，HM 則是 Heatmap，可以看到無論多少資料的情況下 HM 都會比較好，一個可能的理由是 FC 比較容易 overfit ，所以需要更多資料!

Only Pros?? Any cons？

但 Heatmap based 的方法最大的問題就在於速度太慢!如這篇論文中測試出的下圖: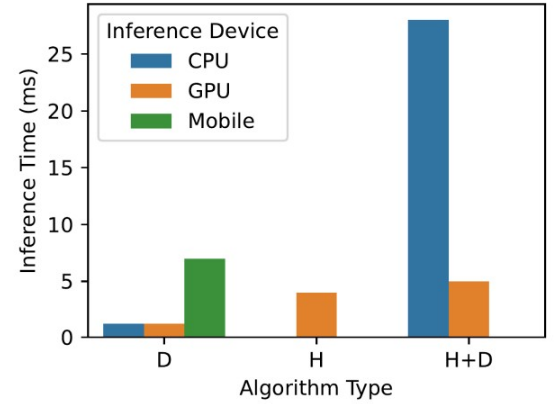

你可以看到 Heatmap 相較於 direct 在執行時資源消耗了非常大！
以詳細的結構來說: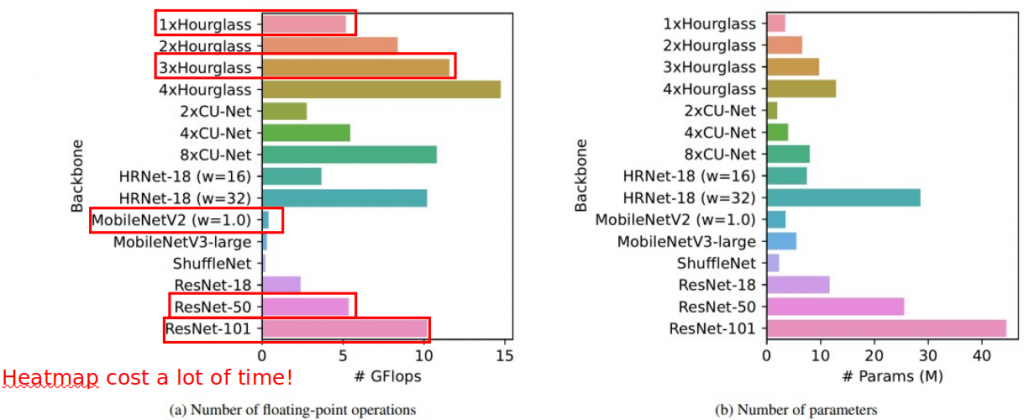

你可以看到慢了不知道幾倍！！而這個也就是 Heatmap 最大的隱憂！如果資源消耗這麼大就算再準可能也上不了終端設備(ex. 手機等等)這樣優勢會受非常大的限制!
那有沒有辦法可以折衷呢？觀察一下上上圖的速度，是不是有看到一個 H+D？對他就是我們明天要來介紹用來改善速度慢的架構！

結語

我們今晚介紹了 heatmap based 的網路結構給大家，但同時也介紹了他可能的問題!那明天我們要來介紹他應用在 Landmark上的改進版本 -- PIPNet 了！

Ref.

1.K Khabarlak, L Koriashkina. Fast facial landmark detection and applications: A survey. arXiv:2101.10808, 2021
2.A. Newell, K. Yang, and J. Deng, “Stacked hourglass networks for human pose estimation,” in European Conference on Computer Vision. Springer, 2016, pp. 483–499.
3.K Khabarlak, L Koriashkina. Fast facial landmark detection and applications: A survey. arXiv:2101.10808, 2021
4.Aiden Nibali, Zhen He, Stuart Morgan, and Luke Prendergast. Numerical coordinate regression with convolutional neural networks. arXiv preprint arXiv:1801.07372, 2018